Programmer en Python en 2nde

Boucle while : encore des exercices

Plus tard ! Les exercices de cette page peuvent être travaillés en seconde lecture.

Fonction mystère

On considère le programme Python suivant : 


def f(x):
    return x**2 - 5*x + 6
	

def g(pas, borne_inf, borne_sup) :
    x = borne_inf
    mini = f(x)
    x_mini = x
	
    while x <= borne_sup : 
        if f(x) < mini :
            x_mini = x
            mini =  f(x)
        x += pas 
		
    return x_mini
	
	
print(g(0.1, -10, 10 ))

Quel affichage peut-on prévoir ? Quel rôle peut jouer la fonction g ?

  • Une réponse
  • Prolongement

Parmi les abscisses borne_inf, borne_inf+pas, borne_inf+2*pas, borne_inf+3*pas, ..., inférieures au égales à borne_sup, la fonction g sélectionne celle qui correspond à une image minimale par f.

Pour des fonctions connues (comme les fonctions du second degré), la fonction g permet de donner une valeur approchée à pas près de l'abscisse en laquelle f admet un minimum (sur [borne_inf; borne_sup]).

En Python, une fonction est un objet comme un autre et peut donc être un paramètre de fonction. On peut donc immédiatement réinvestir le travail avec un second trinôme sans modification de code : 


def trinome1(x):
    return x**2 - 5*x + 6
	
	
def trinome2(x):
    return x**2 + x - 30
	

def g(f,pas, borne_inf, borne_sup) :
    x = borne_inf
    mini = f(x)
    x_mini = x
	
    while x <= borne_sup : 
        if f(x) < mini :
            x_mini = x
            mini =  f(x)
        x += pas 
		
    return x_mini
	
	
print(g(trinome1, 0.1, -10, 10 ))
print(g(trinome2, 0.1, -10, 10 ))

Augmentation relative

  1. Écrire un script Python qui respecte la spécification suivante :
    Saisie Un nombre C > 0
    Affichage Le nombre d'années nécessaires pour doubler le capital C sachant que ce capital augmente de 1% par an.
  2. Le nombre d'années nécessaires pour doubler le capital C dépend-il de la valeur de C ?
  3. En déduire une version du script ne demandant pas la valeur de C.
  • Question 1
  • Question 2
  • Question 3

C = float(input("Entrez la valeur du capital initial (en  kopeks)  : "))
n = 0
nvC = C
while nvC < 2*C :
    n += 1
    nvC *= 1.01
	
print("Le nombre d'années nécessaires pour doubler le capital {} est {}.".format(C, n))
Pour \( C \neq 0 \) : \[ 1{,}01^n C = 2 C \Longleftrightarrow 1{,}01^n = 2 \] 

n = 0
nvC = 1
while nvC < 2  :
    n += 1
    nvC *= 1.01
	
print("Le nombre d'années nécessaires pour doubler le capital est {}.".format(n))

Un classique revisité (bis)

La suite \(u_n\) est définie par \(u_0 = 13\) et, pour tout entier naturel \(n\), par \(u_{n+1} = 0,2 u_n + 0,8\).

Écrire une fonction en Python qui respecte la spécification suivante :

Paramètres un réel u\(_0\) et un entier naturel p
Valeur renvoyée le plus petit entier n tel que u\(_n\) soit proche de 1 à 10\(^{-p}\) près

Compléter le programme par une interaction avec l'utilisateur (saisie d'un entier p puis affichage de l'indice n correspondant).

  • Une solution

			
			
 
		

									
	







 




 










 
 



  Mini exerciseur 2  




	
	
    
	
	
  1. Écrire une fonction en Python
		qui respecte le cahier des charges suivant :
	
	
    
	
    
		Paramètres 
		un entier naturel a et un entier naturel b (non tous deux nuls) 
    
	
    
		Valeur renvoyée
		pgcd(a;b)
	
    
	
    
	
    2. 

	
  2. Écrire un programme qui suit les indications suivantes  :
		
      
			
    •   Un rationnel (positif) est choisi au hasard.
      • 
			
    •   On demande à l'utilisateur d'entrer le numérateur et le
				dénominateur de la fraction irréductible correspondante.
      • 
			 
			
    • Le programme demande à l'utilisateur de recommencer jusqu'à ce
				qu'il réponde correctement à la question.
      • 
		
    	
	
	
    3. 
	









	
    
		
  • Commentaire
    • 
		
  • PGCD
    • 
		
  • Exerciseur
    • 
	

	
 



	

		Comme le Mini exerciseur 1, celui-ci peut-être envisagé comme un
		mini-projet à faire réaliser.
		En plus de programmer pas à pas cet exerciseur, l'élève pourra ensuite
		s'en servir pour s'exercer sur un domaine particulier des mathématiques.
	


		  




		

		

			
		
	
 

		

			

			
			
 
		

									
	






	  


	
	 
	




from random import randint

def pgcd(a,b) :
    while b!=0 :
        a, b = b, a%b
    return a

	
numerateur = randint(1,50)
denominateur = randint(2, 30)

# multiplication pour garantir une fraction réductible : 
coeff =  randint(2,10)
numerateur *= coeff
denominateur *= coeff
d = pgcd(numerateur, denominateur)


while "la réponse donnée n'est pas la bonne" :
	 
    num = int(input("Entrez le numérateur de la fraction irréductible égale à {}/{} : ".format(numerateur, denominateur) ))
    den = int(input("Entrez le dénominateur de la fraction irréductible égale à {}/{} : ".format(numerateur, denominateur) ))
	
    if num * d == numerateur and den * d == denominateur :
        print("Bravo !")
        break					# Sortie anticipée de la boucle
    else :
        print("Essaie encore !")
 








 
 
		





			




 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 




 Multiple de 3 



	

    

  1.  On calcule la somme des chiffres d'un entier naturel n.
	Si le résultat n'est pas compris entre 0 et 9, on calcule la somme de ses
	chiffres. Si le résultat n'est pas entre 0 et 9, on calcule la somme de ses
	chiffres... et ainsi de suite jusqu'à obtenir un résultat entre 0 et 9. 
    
	Écrire une fonction Python qui réalise
	ce travail.
    2. 

  2.  Utiliser la fonction précédente pour rédiger un programme qui renvoie un
	booléen indiquant si un entier naturel est multiple de 3.
    3. 


 
   





	
    
		
  • Jusqu'au chiffre
    • 
		
  • Une solution
    • 
		 
	

	
 
		
	 

  




		

		

			
		
	
 

		

			

			
			
 
		

									
	






 
 






def somme_chiffres(n) :
    """ n est un entier naturel. La fonction renvoie la 
    somme des chiffres de n (en écriture décimale)."""
    if n == 0 :
        return 0
    s = 0
    while n != 0 :
        s += n%10
        n = n//10
    return s
	
	
def jusquau_chiffre(n):
    while n > 9 :
        n = somme_chiffres(n)
    return n
	
	
	
def est_multiple_de_3(n):
    return jusquau_chiffre(n) in (0,3,6,9)
	
print( est_multiple_de_3(123)  )










		

		





			






















 Rendu de monnaie



	

		Écrire une fonction en Python
		qui respecte les spécifications suivantes :
	

	
	

	

		Paramètres 
		un entier naturel non nul (somme à payer) 

			un entier naturel non nul (somme versée par le client)  

	

		Valeur renvoyée
		un triplet contenant le nombre de pièces de 10 euros, de pièces
			de 5 euros et de pièces de 1 euro à rendre sachant que l'on commence
			par rendre le plus de pièces de 10 possible, puis le plus de pièces
			de 5 possible et enfin le reste en pièces de 1.
	

	

	
	

		Tester ensuite le programme avec une somme à payer de 43 euros et un
		versement de 100 euros.
	







	
    
		
  • Une piste
    • 
		
  • Un code possible
    • 
		
  • Une variante
    • 
		
  • Et avec un peu de maths élémentaires
    • 
	

	
 

		  


	Le triplet renvoyé par le fonction sera écrit sous la forme d'un tuple :
	les trois valeurs séparées par une virgule.









def rendu_de_monnaie(somme_due, somme_versee) :
    compteur_10 = 0
    compteur_5 = 0
    compteur_1 = 0
    while somme_versee - somme_due > 0:
        if somme_versee - somme_due >= 10 :
            compteur_10 += 1
            somme_versee -= 10
        elif somme_versee - somme_due >= 5 :
            compteur_5 += 1
            somme_versee -= 5
        else :
            compteur_1 += 1
            somme_versee -= 1
    return compteur_10, compteur_5, compteur_1
	
	
versement =  100
du = 43
d, c, u = rendu_de_monnaie(du, versement)
print("Le versement était de {} euros. La somme due était de {} euros.".format(versement, du))
print("Monnaie rendue : {} pièces de 10, {} pièces de 5, {} pièces de 1.".format(d,c,u))








  


 




def rendu_de_monnaie(somme_due, somme_versee) :
    compteur_10 = 0
    compteur_5 = 0
    compteur_1 = 0
    while somme_versee - somme_due >= 10:
        compteur_10 += 1
        somme_versee -= 10
    while somme_versee - somme_due >= 5 :
        compteur_5 += 1
        somme_versee -= 5
    while somme_versee - somme_due > 0 :
        compteur_1 += 1
        somme_versee -= 1
    return compteur_10, compteur_5, compteur_1
	
	
versement =  100
du = 43
d, c, u = rendu_de_monnaie(du, versement)
print("Le versement était de {} euros. La somme due était de {} euros.".format(versement, du))
print("Monnaie rendue : {} pièces de 10, {} pièces de 5, {} pièces de 1.".format(d,c,u))









	





		
versement =  134
du = 32
 

a_rendre  = versement - du
d = a_rendre//10
a_rendre = a_rendre%10
c = a_rendre//5
a_rendre = a_rendre%5
u = a_rendre


print("Monnaie rendue : {} pièces de 10, {} pièces de 5, {} pièces de 1.".format(d,c,u))



	
		
		

		

		





			




 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 





  Fonction constante par morceaux 



	

 On définit une fonction \(f\) sur \( \left[ 0 ; +\infty\right[ \) par : 



    

  1.  \( f(x) = 0 \)  pour \( x \in [0;1[ \)  (constante sur un intervalle de longueur 1)
    2. 

  2.  \( f(x) = 1 \)  pour \( x \in [1;3[ \)  (constante sur un intervalle de longueur 2)
    3. 

  3.  \( f(x) = 2 \)  pour \( x \in [3;6[ \)  (constante sur un intervalle de longueur 3)
    4. 

  4.  \( f(x) = 3 \)  pour \( x \in [6;10[ \) (constante sur un intervalle de longueur 4)
    5. 

  5.  \( f(x) = 4 \)  pour \( x \in [10;15[ \) (constante sur un intervalle de longueur 5)
    6. 

  6.  ... 
    7. 



 
	

		Écrire une fonction en Python
		qui respecte les spécifications suivantes :
	

	
	

	

		Paramètres 
		un nombre x (de type float)

	

		Valeur renvoyée
		l'image de x par la fonction \(f\)
	

	

	

		Tester ensuite cette fonction sur plusieurs exemples.
	

	
	

 







	
    
		
  • Principe
    • 
		
  • Un code possible
    • 
		
  • Représentation graphique
    • 
	

	
 

  


	
	
Notons  \( T(n) = \sum_{j=0}^{n} j \). 

	
	
Pour tout réel \(x\), il existe un entier (unique) \(n\) tel que \( T(n) \leqslant x < T(n+1) \).
	
	Dès lors, \( f(x) = n \).

	
	 




  


	
	
	




	
def floorTriangulaire(x):
    n = 0
    t = 0
    while t <= x :
        n += 1
        t += n
    return n-1


X = [0, 0.5, 1, 2, 3, 5, 6, 9.8, 10, 12.3, 15, 15.2]
for x in X :
    print( "f({}) = {}.".format(x,floorTriangulaire(x)) )

 









 


	La bibliothèque matplotlib contient des fonctions
	qui permettent de tracer des représentations graphiques. Par contre,
	matplotlib n'est pas une bibliothèque incluse dans la
	distribution usuelle de Python.
	Un « tutoriel » pour installer des modules supplémentaires
	est disponible à la page
	[Sources] → [Modules complémentaires]).


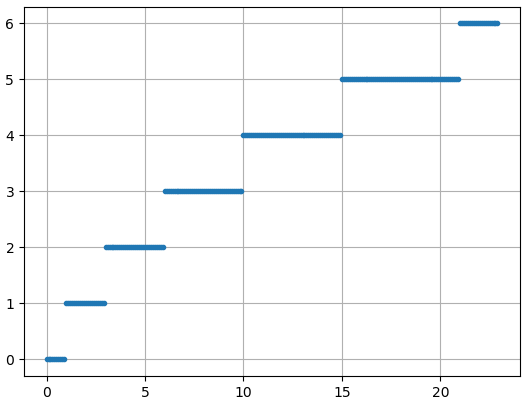
Représentation graphique de f


	Voici les éléments de code permettant d'obtenir la représentation graphique ci-dessus :








from pylab import plot, show, axis, grid 
from numpy import arange


def floorTriangulaire(x):
    n = 0
    t = 0
    while t <= x :
        n += 1
        t += n
    return n-1

 

X = arange(0, 23, 0.1) # liste [0, 0+0.1, 0+2*0.1, 0+3*0.1, ..., 22.9]
Y = [ floorTriangulaire(x)  for x  in X] # liste des images 

# construction du graphique :
plot(X, Y,'.')
# tracé d'une grille en fond :
grid()
# pour voir le résultat :
show()