Entrée, sortie et fonction

Les notions d'entrée et de sortie sont naturellement attachées à la notion de fonction.

Dans le cas des fonctions, on précisera souvent en parlant des paramètres d'entrée (on parle aussi d' "arguments" de la fonction dans la littérature informatique) et des valeurs renvoyées (on trouve aussi "valeur retournée" dans la littérature informatique, il s'agit a priori d'une mauvaise traduction de l'anglais return).

Rôle des fonctions en programmation

Un rôle en classe de seconde pourra être de coder une fonction mathématique.
Un rôle essentiel des fonctions en programmation est d'organiser le code en petites unités logiques, en petites unités de traitement aux rôles bien distincts. Ce découpage facilite la lecture d'un programme (et en facilite la maintenance).
Un autre rôle essentiel est de factoriser le code, c'est-à-dire d'éviter d'avoir à écrire à plusieurs endroits du programme des bouts de code similaires.

Spécifier une fonction

Dans la suite de ces pages, nous utiliserons l'expression spécifier une fonction. Il s'agira de :

préciser quelles sont les données d'entrée,
préciser quel est le résultat renvoyé,
quelles sont les propriétés qui relient les données et le résultat.

Spécifier une fonction, c'est donc en donner le cahier des charges : que calcule-t-elle et à partir de quelles entrées ? Par contre, la spécification ne s'occupe pas de dire comment se fait ce calcul (notamment la spécification n'explicite pas d'algorithme).

La phase de spécification est donc suivie d'une phase d'implantation (on trouve aussi le mot implémentation). En informatique, on parle en général à ce stade de définir la fonction : c'est le comment. Une même spécification peut donc donner lieu à plusieurs implantations.

Dans un travail informatique, si l'on veut que les élèves utilisent une fonction sans la définir eux-mêmes (par exemple parce que ce serait trop difficile ou trop long, ou déjà réalisé quelques semaines auparavant...), il sera nécessaire de préciser la spécification de cette fonction aux élèves (la spécification peut alors être considérée comme un mode d'emploi de la fonction), mais il n'est pas besoin d'en préciser la définition (c'est-à-dire comment le calcul permettant de transformer les entrées en sortie est construit).

Exemple

Définir une fonction spécifiée comme suit :

Paramètre	Un entier relatif n.
Valeur renvoyée	True si n est racine du trinôme \( x \longmapsto x^2 - x - 6 \), False sinon.

Deux fonctions, définies différemment et satisfaisant cette spécification :

def est_racine(n):
    return n*n - n - 6 == 0

print(est_racine(3))
print(est_racine(4))

def est_racine(n):
    return n == -2 or n == 3

print(est_racine(3))
print(est_racine(4))

Définir une fonction en langage Python

Prenons l'exemple d'une fonction prenant en entrée un nombre x (c'est-à-dire une variable de type float ou de type int) et renvoyant en sortie le carré de x.

Au collège, avec le langage Scratch, les élèves définissaient cette fonction ainsi :

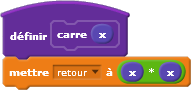
En Python, la même fonction sera définie comme ci-dessous :


def carre(x):
    return x*x

Le mot clef def annonce que le nom qui suit (ici carre) sera une fonction.
On indique ensuite entre parenthèses le ou les paramètres (il peut ne pas y avoir de paramètre).
Les deux points « : » permettent de déclarer le début du bloc d'instructions qui composent cette fonction. Ce bloc doit obligatoirement être indenté.
On indique l'image (ce que renvoie la fonction) grâce au mot-clef return (il peut ne pas y avoir d'image).

Faire appel à une fonction

A ce stade, on a seulement défini la fonction. Il reste à appeler cette fonction pour calculer effectivement le carré d'un nombre.

Essayez d'exécuter le code ci-dessous. Que se passe-t-il ?

def carre(x):
    return x*x
	
carre(3)

La ligne carre(3) est un appel à la fonction carre. L'exécution du script va lire le code de la fonction carre en remplaçant le paramètre x par 3, et va donc renvoyer 3*3, c'est à dire 9.

Pourtant il semble ne rien se passer lorsqu'on exécute ce code. C'est normal, on a demandé de calculer l'image de 3 par la fonction mais on n'a pas demandé à Python d'en faire quelque chose. Python calcule donc carre(3) et s'arrête.

On pourrait par exemple demander à Python d'afficher le résultat :

def carre(x):
    return x*x
	
print(carre(3))

On pourrait aussi demander au programme d'utiliser ce résultat dans un calcul :

def carre(x):
    return x*x
	
a = carre(3) + 5
print(a)

Ordre de lecture

Voici un exercice donné en classe à des élèves de seconde :

On considère la fonction ci-dessous, définie en langage Python :


def e(a, b):
    a = a+b
    b = a-b
    a = a-b
    return a, b

Que renvoie l'instruction e(5, 2) ?
Que renvoie l'instruction e(-8, 4) ?
Que semble réaliser cette fonction ?
Prouver mathématiquement cette conjecture.
Quel nom plus explicite aurait-on pu donner à la fonction e ?

Et voici la suite en salle informatique :

Afin qu'ils s'habituent à la syntaxe du langage, il a été demandé aux élèves de concevoir une interaction avec l'utilisateur. Voici le programme qui en a résulté :

def echange(a, b):
    a = a+b
    b = a-b
    a = a-b
    return a, b

##----- interaction -----##
x = float(input("Entrez le premier nombre : "))
y = float(input("Entrez le second nombre : "))
x, y = echange(x, y)
print("Alors x = {} et y = {}.".format(x, y))

Lors de la mise en commun, un élève a posé la question :

« Pourquoi le programme ne fonctionne-t-il pas dans l'ordre ? »

Il sous-entendait par là l'ordre de lecture, c'est-à-dire l'ordre des numéros de lignes. Réponse apportée aux élèves : " très souvent un exercice de mathématiques définit une fonction en début d'énoncé même si celle-ci n'est « utilisée » qu'à la 2^ème ou à la 3^ème question... "

La page suivante (dernier exemple) donne un autre argument susceptible d'expliquer ce problème d'ordre lors de l'utilisation des fonctions. En sauvegardant et en exécutant un programme contenant uniquement la définition de la fonction echange(), celle-ci est « mise en attente », hors du flux de l'interpréteur. La fonction echange() ne revient dans le flux d'exécution que lorsqu'on y fait appel.