Tétraminos - Une solution

La réponse à la question du défi est négative.
En voici une démonstration… par coloriage !

Remarque

Ce défi a été donné à des élèves à différents niveaux d’enseignement, souvent sous forme de narration de recherche. Pour qui avaient rendu une copie, les réponses étaient diverses :

• une démonstration par exhaustion des cas pour montrer l’impossibilité,
• « j’ai essayé plusieurs fois et je n’y suis pas arrivé donc il n’y a pas de solution »,
• etc…

Montrer la démonstration de cette impossibilité par coloriage permet de mettre en avant qu’une démonstration n’est pas limitée à un exercice de géométrie en collège et qu’elle n'est pas forcément standardisée et immuable : il existe divers types de démonstration !
De plus, l’idée de prendre cinq pièces plutôt que sept repose sur une manipulation plus rapide.

Démonstration

D’un côté, colorions le rectangle comme un damier de jeu de dames ou d’échecs : les cases seront coloriées de deux couleurs différentes, par exemple bleu clair et bleu foncé.

D'un autre côté, colorions de la même façon les cinq pièces.
Quatre pièces auront deux cases bleu clair et deux cases bleu foncé, tandis qu’une cinquième (le « T ») aura trois cases bleu clair et une case bleu foncé (ou une case bleu clair et trois cases bleu foncé) :

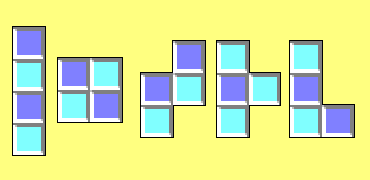
Par conséquent, le nombre total de cases bleu ciel sera 4 * 2 + 3, soit 11 (ou 4 * 2 + 1, soit 9).

Il n’y a pas le même nombre de cases bleu clair dans les deux coloriages, ce qui montre l’impossibilité d’un tel recouvrement.

Compléments

De même, si l’on utilise l’ensemble des sept pièces données au début, il y a un total de 28 carrés unitaires.
Il faudrait donc un rectangle de quatorze cases de chacune des deux couleurs.

Or l’ensemble des pièces a quinze carrés d’une couleur et treize de l’autre.
L’impossibilité est encore montrée.