2020, année mathémagique - Une solution
2020, année mathémagique - Une solution
Les entiers naturels $p$ et $q$ (non nul) étant donnés, il est rapide de vérifier que, si la roue $R$ est magique, alors la figure $R’ = p + q R$ (où chaque entier $N$ de $R$ est associé à l’entier $N’ = p + q N$ de $R’$) est aussi magique.
Il « suffit » donc de trouver deux entiers $p$ et $q$ (non nuls) qui répondent au problème.
La nature affine de l’expression $p + q N$ fait penser à une suite arithmétique !
Ainsi, une piste est de trouver une suite arithmétique $(Un)$ telle que
$U_a + U_b + U_c = 2 020$, où les trois indices $a$, $b$ et $c$ sont justement les
trois nombres de chaque alignement. Autrement dit, ils vérifient l’égalité
$a + b + c = 19$.
En définissant de façon usuelle le terme général $U_n$ par $U_n = U_0 + r n$
(ce qui explique au passage le choix de commencer la liste des entiers à $0$
et non pas à $1$), il vient :
$$U_a + U_b + U_c = U_0 + r a + U_0 + r b + U_0 + r c = 3 U_0 + (a+ b + c) r = 3 U_0 + 19 r$$
Or $U_a + U_b + U_c = 2 020$.
Donc $3 U_0 + 19 r = 2 020$, ce qui équivaut à
$U_0 = (2 020 – 19 r) \div 3$.
Puisque $U_0$ est entier et positif, une méthode consiste à tester, pour chacun des
entiers $r$ allant de $1$ au quotient entier de $2020$ par $19$ augmenté de $1$,
si $U_0$ est entier et d’afficher alors le couple $(U_0 , r)$.
Les deux entiers $p$ et $q$ cherchés seront alors $p = U_0$ et $q = r$.
On va écrire en langage Python un programme qui permette d’obtenir des couples
$(U_0 , r)$ solutions que la variable $t$ permet de dénombrer.
Rappel : Le quotient entier est obtenu grâce à la contre-oblique
// :

L’exécution de ce programme donne trente-six couples solutions (ce qui, au passage, permet d’offrir à chacun des élèves d’une classe une roue différente !) :

Prenons, par exemple, le vingt-septième couple proposé, (173, 79).
Chaque entier $N$ de la première roue va donner l’entier $N’ = 173 + 79 N$ de
la seconde roue. Ainsi, à $4$ est associé $173 + 79 \times 4 = 489$ et à $9$ est
associé $173 + 79 \times 9 = 884$.
On complète le programme précédent par une fonction roue, de paramètres
$p$ et $q$, qui renvoie les dix-neuf valeurs demandées :

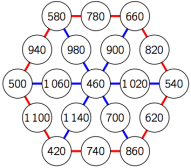
Évidemment, l’exécution de roue(0, 1) donne la roue initiale !
L’exécution de roue(173, 79) donne les dix-neuf valeurs qui construisent la roue suivante :
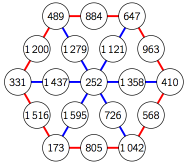
De même, l’exécution de roue(420, 40) donne celles qui construisent la roue suivante ::