Les plans colorés - Une solution

On peut déjà remarquer que si une seule couleur est effectivement utilisée, alors elle est évidemment complète. On peut donc se placer a priori dans le cas où il existe des points verts et des points rouges.

On raisonne par l'absurde: on suppose que les deux couleurs sont incomplètes et on montre que cela mène à une contradiction.

Si les deux couleurs ne sont pas complètes, il existe un réel $v > 0 $ tel que la distance entre deux points verts n'est jamais $v$ et il existe un réel $r > 0$ tel que la distance entre deux points rouges n'est jamais $r$.
On a soit $r ≤ v$, soit $v < r$.

Cas où $r ≤ v$

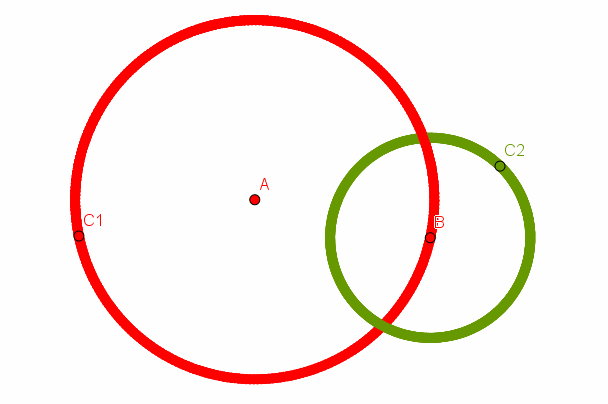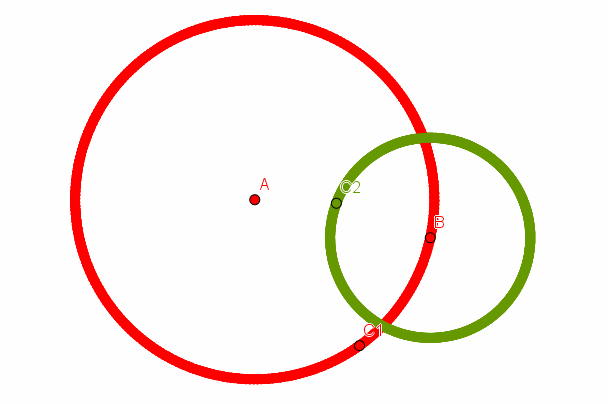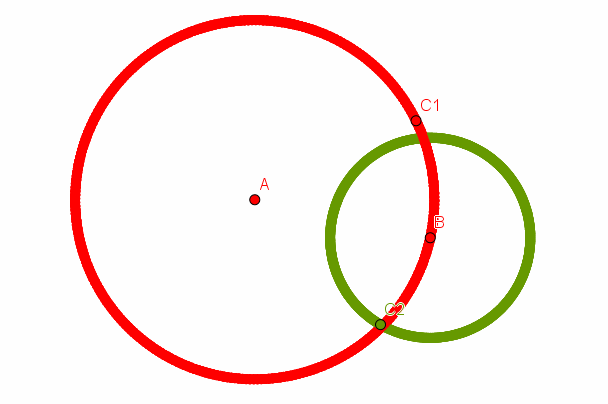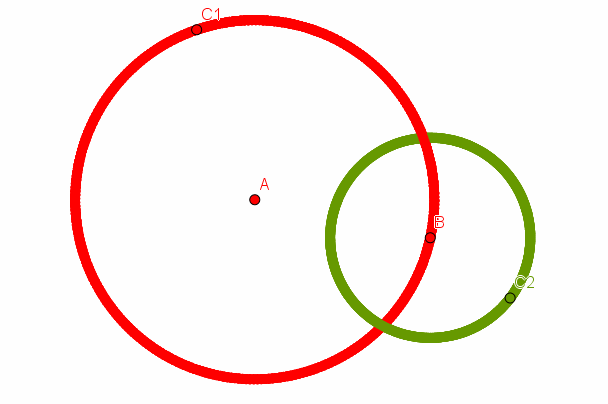
Soit $A$ un point vert.
On trace un cercle $C_1$ de centre $A$ et de rayon $v$. Ce cercle est uniquement constitué de points rouges (car avec un point $B$ vert sur ce cercle, on aurait une distance $AB = v$ entre deux points verts, ce qui est impossible d'après notre hypothèse).

Prenons alors un point $B$ sur ce cercle et traçons un cercle $C_2$ de centre $B$ et de rayon $r$. Ce cercle est entièrement vert (car avec un point $C$ rouge sur ce cercle, on aurait une distance $BC = r$ entre deux points rouges, ce qui est impossible par notre hypothèse).

Comme $r ≤ v$, le cercle $C_2$ coupe $C_1$. Mais à l'intersection des deux cercles, on aurait donc des points à la fois vert et rouge. Contradiction.

Cas où $r > v$

On montre de la même façon que cette situation est impossible.

Conclusion

L'une des deux couleurs au moins est complète.